Geometry Puzzle - Grid and Circle - Solution

Winner: Nanpeng!

Solution:
r = √12.5   = 5/2 * √2

The first trick to finding this solution is to realize that the circle does not need to be centered on a grid intersection.

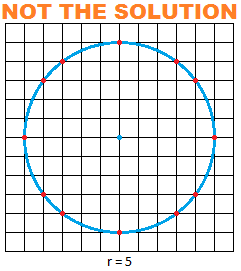
To understand how you might solve problems like this, you can start by understanding this circle:

To me, this is the most obvious potential solution.  The circle passes through 12 grid intersections, and so is a candidate for the solution to the problem.  This circle is based on the well known 3-4-5 triangle.  Because 3² + 4² = 5², the distance from the center to any of the 8 points near the corners is 5, the same as the distance to the 4 points near the edges.

The solution is actually just a rotated and shrunken version of this.  Observe:

 This is the r=5 circle from above.  I have overlaid a diagonal grid in green.  You can see that if you look only at the green grid, this circle is identical to the solution.

There are other ways you could find the actual solution.  One of them is to realize that 7² + 1² = 5² + 5².  The points near the corners are 5 half-units from center of the circle horizontally, and 5 half-units vertically as well.  The points near the edges are 7 half-units one way and 1 half-unit the other.  Therefore, they are all the same distance from the center.  This is actually the way I did it when I invented the puzzle.



Additional Information

I used my mad programming skills to generate a list of circles with notable point counts (with radii less than 10000).  The data is below.  I considered only circles centered on grid intersections, in the middle of grid squares, or in the middle of grid edges (not pictured above).  Each entry in the list looks like this:

    point count: radius
         x1, y1
         x2, y2
         ...
(Mirror-image coordinates are not listed.  For instance, the circle with a point count of 4 and radius of 1 actually has these points: (0,1), (0,-1), (1,0) and (-1,0).  I only listed one of these since the rest can be easily inferred.)
(for circles centered on squares or edges, the coordinates should be divided by two to get actual non-integer coordinates)

A circle is listed if and only if it has a higher point count than all smaller circles in that category.

A couple interesting things are visible in the data:

1. For every circle centered on a grid intersection, there is a corresponding circle centered in the middle of a square.  (they are shown side-by-side in the table)  This circle has the same point count but the radius is smaller by a factor of the square root of two.
• The points in these circles are related on a sum-and-difference basis.  So, for the 3-4-5 circle from above, the points are 4,3 and 5,0.  The sum of 4 and 3 is 7, and the difference of 4 and 3 is 1.  So, 7,1 is a point in the corresponding circle.  Similarly, the sum of 0 and 5 is 5 and the difference of 0 and 5 is 5.  So, 5,5 is a point in the corresponding circle.
2. For every circle centered on a grid intersection, there is a corresponding circle centered on the middle of an edge.  This circle has half the point count and half the radius.
3. The point counts do not increase by 4 each time.  The pattern of increasing point counts appears to be irregular.

The bottom line is that circles centered on grid squares will always win in puzzles like this one.


Circles centered on  Circles centered on  Circles centered on
grid intersections:  grid squares:        grid edges:
    4: 1.00000           4: 0.70711           2: 0.50000
        1, 0                 1, 1                 1, 0
    8: 2.23607           8: 1.58114           4: 1.11803
        2, 1                 3, 1                 2, 1
   12: 5.00000          12: 3.53553           6: 2.50000
        4, 3                 5, 5                 4, 3
        5, 0                 7, 1                 5, 0
   16: 8.06226          16: 5.70088           8: 4.03113
        7, 4                 9, 7                 7, 4
        8, 1                 11, 3                8, 1
   24: 18.02776         24: 12.74755         12: 9.01388
        15, 10               19, 17               15, 10
        17, 6                23, 11               17, 6
        18, 1                25, 5                18, 1
   32: 33.24154         32: 23.50532         16: 16.62077
        24, 23               37, 29               24, 23
        31, 12               41, 23               31, 12
        32, 9                43, 19               32, 9
        33, 4                47, 1                33, 4
   36: 65.00000         36: 45.96194         18: 32.50000
        52, 39               65, 65               52, 39
        56, 33               79, 47               56, 33
        60, 25               85, 35               60, 25
        63, 16               89, 23               63, 16
        65, 0                91, 13               65, 0
   48: 74.33034         48: 52.55949         24: 37.16517
        55, 50               81, 67               55, 50
        62, 41               87, 59               62, 41
        70, 25               93, 49               70, 25
        71, 22               95, 45               71, 22
        73, 14               103, 21              73, 14
        74, 7                105, 5               74, 7
   64: 166.20770        64: 117.52659        32: 83.10385
        120, 115             185, 145             120, 115
        132, 101             191, 137             132, 101
        141, 88              205, 115             141, 88
        144, 83              215, 95              144, 83
        155, 60              227, 61              155, 60
        160, 45              229, 53              160, 45
        164, 27              233, 31              164, 27
        165, 20              235, 5               165, 20
   72: 268.00187        72: 189.50594        36: 134.00093
        191, 188             269, 267             191, 188
        208, 169             305, 225             208, 169
        215, 160             325, 195             215, 160
        236, 127             333, 181             236, 127
        247, 104             351, 143             247, 104
        257, 76              363, 109             257, 76
        260, 65              375, 55              260, 65
        265, 40              377, 39              265, 40
        268, 1               379, 3               268, 1
   80: 371.65172        80: 262.79745        40: 185.82586
        275, 250             393, 349             275, 250
        301, 218             405, 335             301, 218
        310, 205             435, 295             310, 205
        317, 194             465, 245             317, 194
        334, 163             475, 225             334, 163
        350, 125             497, 171             350, 125
        355, 110             511, 123             355, 110
        365, 70              515, 105             365, 70
        370, 35              519, 83              370, 35
        371, 22              525, 25              371, 22
   96: 400.28115        96: 283.04152        48: 200.14058
        300, 265             415, 385             300, 265
        311, 252             431, 367             311, 252
        329, 228             469, 317             329, 228
        337, 216             473, 311             337, 216
        356, 183             497, 271             356, 183
        360, 175             515, 235             360, 175
        375, 140             535, 185             375, 140
        384, 113             539, 173             384, 113
        392, 81              553, 121             392, 81
        393, 76              557, 101             393, 76
        399, 32              563, 59              399, 32
        400, 15              565, 35              400, 15
  128: 895.05586       128: 632.90007        64: 447.52793
        655, 610             905, 885             655, 610
        703, 554             985, 795             703, 554
        710, 545             1013, 759            710, 545
        722, 529             1039, 723            722, 529
        766, 463             1067, 681            766, 463
        769, 458             1095, 635            769, 458
        785, 430             1103, 621            785, 430
        815, 370             1165, 495            815, 370
        830, 335             1185, 445            830, 335
        862, 241             1215, 355            862, 241
        865, 230             1227, 311            865, 230
        874, 193             1229, 303            874, 193
        881, 158             1251, 193            881, 158
        886, 127             1255, 165            886, 127
        890, 95              1257, 149            890, 95
        895, 10              1265, 45             895, 10
  144: 1443.23422      144: 1020.52070       72: 721.61711
        1027, 1014           1469, 1417           1027, 1014
        1107, 926            1571, 1303           1107, 926
        1133, 894            1597, 1271           1133, 894
        1170, 845            1625, 1235           1170, 845
        1230, 755            1735, 1075           1230, 755
        1245, 730            1765, 1025           1245, 730
        1261, 702            1807, 949            1261, 702
        1322, 579            1873, 811            1322, 579
        1331, 558            1879, 797            1331, 558
        1338, 541            1889, 773            1338, 541
        1342, 531            1901, 743            1342, 531
        1378, 429            1963, 559            1378, 429
        1395, 370            1975, 515            1395, 370
        1405, 330            1985, 475            1405, 330
        1430, 195            2015, 325            1430, 195
        1434, 163            2027, 239            1434, 163
        1437, 134            2033, 181            1437, 134
        1443, 26             2041, 13             1443, 26
  160: 2001.40576      160: 1415.20758       80: 1000.70288
        1483, 1344           2075, 1925           1483, 1344
        1500, 1325           2143, 1849           1500, 1325
        1555, 1260           2155, 1835           1555, 1260
        1604, 1197           2309, 1637           1604, 1197
        1645, 1140           2345, 1585           1645, 1140
        1685, 1080           2365, 1555           1685, 1080
        1692, 1069           2429, 1453           1692, 1069
        1780, 915            2485, 1355           1780, 915
        1800, 875            2531, 1267           1800, 875
        1811, 852            2575, 1175           1811, 852
        1875, 700            2663, 959            1875, 700
        1899, 632            2675, 925            1899, 632
        1920, 565            2695, 865            1920, 565
        1941, 488            2761, 623            1941, 488
        1960, 405            2765, 605            1960, 405
        1965, 380            2785, 505            1965, 380
        1973, 336            2801, 407            1973, 336
        1995, 160            2815, 295            1995, 160
        1996, 147            2825, 175            1996, 147
        2000, 75             2827, 139            2000, 75
  192: 2434.81519      192: 1721.67433       96: 1217.40759
        1746, 1697           2497, 2371           1746, 1697
        1806, 1633           2527, 2339           1806, 1633
        1823, 1614           2633, 2219           1823, 1614
        1890, 1535           2711, 2123           1890, 1535
        1953, 1454           2725, 2105           1953, 1454
        1985, 1410           2855, 1925           1985, 1410
        2065, 1290           2875, 1895           2065, 1290
        2110, 1215           2953, 1771           2110, 1215
        2118, 1201           3025, 1645           2118, 1201
        2191, 1062           3061, 1577           2191, 1062
        2202, 1039           3131, 1433           2202, 1039
        2238, 959            3149, 1393           2238, 959
        2271, 878            3197, 1279           2271, 878
        2282, 849            3241, 1163           2282, 849
        2319, 742            3253, 1129           2319, 742
        2335, 690            3319, 917            2335, 690
        2362, 591            3325, 895            2362, 591
        2385, 490            3355, 775            2385, 490
        2390, 465            3395, 575            2390, 465
        2415, 310            3407, 499            2415, 310
        2417, 294            3425, 355            2417, 294
        2426, 207            3437, 209            2426, 207
        2433, 94             3439, 173            2433, 94
        2434, 63             3443, 49             2434, 63
  256: 5444.41227      256: 3849.78084      128: 2722.20614
        3896, 3803           5511, 5377           3896, 3803
        3980, 3715           5567, 5319           3980, 3715
        4027, 3664           5721, 5153           4027, 3664
        4133, 3544           5755, 5115           4133, 3544
        4156, 3517           5935, 4905           4156, 3517
        4280, 3365           5997, 4829           4280, 3365
        4315, 3320           6215, 4545           4315, 3320
        4520, 3035           6315, 4405           4520, 3035
        4540, 3005           6495, 4135           4540, 3005
        4645, 2840           6665, 3855           4645, 2840
        4772, 2621           6705, 3785           4772, 2621
        4805, 2560           6837, 3541           4805, 2560
        4861, 2452           6935, 3345           4861, 2452
        4931, 2308           6957, 3299           4931, 2308
        4960, 2245           7051, 3093           4960, 2245
        5051, 2032           7071, 3047           5051, 2032
        5059, 2012           7083, 3019           5059, 2012
        5072, 1979           7205, 2715           5072, 1979
        5128, 1829           7239, 2623           5128, 1829
        5140, 1795           7313, 2409           5140, 1795
        5189, 1648           7365, 2245           5189, 1648
        5245, 1460           7393, 2151           5245, 1460
        5260, 1405           7485, 1805           5260, 1405
        5315, 1180           7545, 1535           5315, 1180
        5360, 955            7555, 1485           5360, 955
        5380, 835            7635, 995            5380, 835
        5413, 584            7645, 915            5413, 584
        5420, 515            7673, 639            5420, 515
        5435, 320            7677, 589            5435, 320
        5437, 284            7691, 363            5437, 284
        5443, 124            7695, 265            5443, 124
        5444, 67             7699, 93             5444, 67
  288: 8778.85101      288: 6207.58508      144: 4389.42550
        6240, 6175           9035, 8515           6240, 6175
        6497, 5904           9223, 8311           6497, 5904
        6625, 5760           9335, 8185           6625, 5760
        6663, 5716           9389, 8123           6663, 5716
        6740, 5625           9565, 7915           6740, 5625
        6864, 5473           9893, 7501           6864, 5473
        7111, 5148           9971, 7397           7111, 5148
        7176, 5057           10231, 7033          7176, 5057
        7353, 4796           10427, 6739          7353, 4796
        7428, 4679           10477, 6661          7428, 4679
        7487, 4584           10561, 6527          7487, 4584
        7521, 4528           10663, 6359          7521, 4528
        7568, 4449           10729, 6247          7568, 4449
        7692, 4231           10853, 6029          7692, 4231
        7839, 3952           10985, 5785          7839, 3952
        7865, 3900           11219, 5317          7865, 3900
        8000, 3615           11335, 5065          8000, 3615
        8100, 3385           11435, 4835          8100, 3385
        8135, 3300           11485, 4715          8135, 3300
        8200, 3135           11615, 4385          8200, 3135
        8268, 2951           11765, 3965          8268, 2951
        8385, 2600           11791, 3887          8385, 2600
        8441, 2412           11923, 3461          8441, 2412
        8488, 2241           12017, 3119          8488, 2241
        8511, 2152           12049, 2993          8511, 2152
        8544, 2017           12071, 2903          8544, 2017
        8569, 1908           12107, 2749          8569, 1908
        8583, 1844           12149, 2557          8583, 1844
        8632, 1599           12233, 2119          8632, 1599
        8684, 1287           12259, 1963          8684, 1287
        8697, 1196           12337, 1391          8697, 1196
        8740, 825            12365, 1115          8740, 825
        8756, 633            12379, 947           8756, 633
        8760, 575            12385, 865           8760, 575
        8767, 456            12401, 593           8767, 456
        8775, 260            12415, 65            8775, 260
                       320: 8608.37165      160: 6087.03797
                             12217, 12131         8730, 8485
                             12485, 11855         8786, 8427
                             12635, 11695         9030, 8165
                             13121, 11147         9083, 8106
                             13165, 11095         9115, 8070
                             13237, 11009         9450, 7675
                             13555, 10615         9547, 7554
                             13625, 10525         9765, 7270
                             13919, 10133         9925, 7050
                             14275, 9625          10014, 6923
                             14375, 9475          10242, 6581
                             14707, 8951          10325, 6450
                             14765, 8855          10550, 6075
                             15019, 8417          10590, 6005
                             15125, 8225          10762, 5691
                             15305, 7885          10821, 5578
                             15491, 7513          10955, 5310
                             15655, 7165          11010, 5195
                             15745, 6965          11158, 4869
                             15943, 6499          11190, 4795
                             15985, 6395          11221, 4722
                             16027, 6289          11355, 4390
                             16205, 5815          11410, 4245
                             16265, 5645          11502, 3989
                             16399, 5243          11595, 3710
                             16453, 5071          11675, 3450
                             16595, 4585          11718, 3301
                             16625, 4475          11810, 2955
                             16775, 3875          11829, 2878
                             16823, 3661          11925, 2450
                             16937, 3091          11950, 2325
                             16975, 2875          12026, 1893
                             17035, 2495          12075, 1550
                             17101, 1993          12085, 1470
                             17125, 1775          12123, 1114
                             17185, 1045          12130, 1035
                             17189, 977           12134, 987
                             17195, 865           12165, 470
                             17213, 359           12170, 315
                             17215, 245           12174, 43
                                            192: 7795.21207
                                                  11138, 10909
                                                  11210, 10835
                                                  11302, 10739
                                                  11789, 10202
                                                  11885, 10090
                                                  11918, 10051
                                                  11990, 9965
                                                  12403, 9446
                                                  12422, 9421
                                                  12541, 9262
                                                  12790, 8915
                                                  12958, 8669
                                                  12986, 8627
                                                  13261, 8198
                                                  13315, 8110
                                                  13373, 8014
                                                  13474, 7843
                                                  13747, 7354
                                                  13810, 7235
                                                  13885, 7090
                                                  14003, 6854
                                                  14074, 6707
                                                  14174, 6493
                                                  14435, 5890
                                                  14477, 5786
                                                  14515, 5690
                                                  14563, 5566
                                                  14710, 5165
                                                  14806, 4883
                                                  14867, 4694
                                                  14990, 4285
                                                  15026, 4157
                                                  15082, 3949
                                                  15166, 3613
                                                  15203, 3454
                                                  15235, 3310
                                                  15362, 2659
                                                  15389, 2498
                                                  15394, 2467
                                                  15410, 2365
                                                  15469, 1942
                                                  15485, 1810
                                                  15518, 1501
                                                  15562, 941
                                                  15565, 890
                                                  15571, 778
                                                  15581, 542
                                                  15590, 115

Geometry Puzzle - Grid and Circle

You have a sheet of graph paper and a compass. Draw a circle that passes through more than 8 grid intersections. Specifically, draw the smallest possible such circle.

For example, the following circle only passes through 8 grid intersections, and so is not a solution. 

To post your answer, just post a comment with the radius of the circle (please do not post an image).  For example, if you were posting the example above as an answer, post "r=square root of 5" or similar text.  I will post the correct answer (and winner) as another blog post.

(FYI, this has also been posted on Facebook.  Facebook comments will also be in the running to win.)





















Adding whitespace so you have to scroll down to see the solution in the comments.


























Whitespace complete.

51 Star Flag (continued)

A previous post on this blog discussed the mathematics of grid and checkerboard flags. These are suitable for most numbers of stars, including 51. Occasionally, however, these techniques are not sufficient. For instance, there are no suitable grid/checkerboard flags for 62, 79 or 89 stars. You may also just get bored of checkerboard and grid flags and want something different. As it turns out, there are plenty of options. Without further ado:

Alternative Flag Styles

The first five styles were actually used for US flags. They are named after the state that whose joining caused that flag. The other styles have never been used, but are valuable mathematically.

Michigan style is a simple grid flag with an extra star in the top and bottom rows.
Number of stars = rows x columns + 2

Oregon style is a simple grid flag with two stars removed from the center row. (though it only looks good if the number of rows is odd, so that the the modified row can be centered)
Number of stars = rows x columns - 2

Kansas is like Oregon except that it only has one star removed.
Number of stars = rows x columns - 1

Nevada is the most complicated design so far. The best way to look at it is to mentally combine the left and right columns and make a simple grid flag with one extra star. (But only if the number of rows is odd)
Number of stars = rows x columns + 1

Mathematical trick for Nevada

Colorado is a simple grid with a star removed from the top and bottom rows. This gives it the same math as Oregon, but with no odd rows restriction.
Number of stars = rows x columns - 2

No Corners is the heaviest modification so far. It is a grid with four stars removed.
Number of stars = rows x columns - 4

Modified Checkerboard can be best thought of as a checkerboard flag with an extra star added to the left and right columns. This design only works if it is based on an odd x odd checkerboard pattern with corners black (see previous post for checkerboard flag analysis).
Number of stars = (rows x columns - 1) / 2 + 2 
                        (Checkerboard with black corners, plus 2)

This gives us an army of new formulas with which to do our flag hunting. Solving them all for rows x columns we get:

rows x columns = (Number of stars) - 2       Michigan
rows x columns = (Number of stars) - 1       Nevada
rows x columns = (Number of stars) + 1       Kansas
rows x columns = (Number of stars) + 2       Oregon or Colorado
rows x columns = (Number of stars) + 4       No Corners
rows x columns = (Number of stars) x 2 - 3   Modified Checkerboard

From the last post:
rows x columns = (Number of stars) x 2       Even checkerboard flags
rows x columns = (Number of stars) x 2 - 1   Odd checkerboard, white corners
rows x columns = (Number of stars) x 2 + 1   Odd checkerboards, black corners
rows x columns = (Number of stars)           Simple grid flags

The procedure for finding a flag with a given number of stars is to use these formulas to find possible values of rows x columns for your given number of stars. Then, try to factor rows x columns into appropriate values for rows and columns.

For 62, this gives us:
Michigan:                  62 - 2 = 60 = 6 x 10
Nevada:                    62 - 1 = 61 = PRIME
Kansas:                    62 + 1 = 63 = 7 x 9
Oregon/Colorado:           62 + 2 = 64 = 8 x 8 
                              (Oregon requires odd rows, though)
No Corners:                62 + 4 = 66 = 6 x 11
Mod. Check:                62 x 2 - 3 = 121 = 11 x 11
Even Check:                62 x 2 = 124 = 4 x 31 UGLY
Odd Check, White Corners:  62 x 2 - 1 = 123 = 3 x 41 UGLY
Odd Check, Black Corners:  62 x 2 + 1 = 125 = 5 x 25 UGLY
Simple Grid:               62 = 2 x 31 UGLY

This gives us five options for a 62 star flag:

There are other flag designs that could be imagined, but this collection gives us plenty of formulas to work with, and all of the patterns are aesthetically pleasing.

The last post mentioned that 62, 79 and 89 are hard to find flag patterns for.  62 has been done just now.  Here are suitable patterns for 79 and 89, using the mathematics described above.

A nice article from Slate (www.slate.com) and a fun widget from PopSci (www.popsci.com) about this topic do not have solutions for 29, 69 and 87 stars.  With the mathematics described above, we can find patterns for all of them.

With this I bring you my final set of options for a 51 star flag:

The mathematics I have so far described gives us Checkerboard, Michigan and Modified Checkerboard styles.  The Checkerboard style is the currently accepted design if Puerto Rico should become a state.  I add two other styles here.  One is the Special Circular.  51 happens to be an excellent number to arrange in a circle.  The circular pattern is a popular alternative to the accepted checkerboard and it was not designed by this blog.  The 'Special' pattern is my own invention, and it has a lot of interesting mathematics behind it.  It is actually a further modification of the idea of a checkerboard flag.  But those mathematics are for another post :-)

51 Star Flag

The United States Flag is beautiful.  Throughout our country's history, the flag has changed many times.  The general concept remained the same, but the number of stars has changed repeatedly as new states were added.  This gave the country an interesting mathematical challenge - how to arrange n stars in a rectangle in an aesthetically pleasing way.  America may once again be faced with this challenge if Puerto Rico becomes a state.  I think that many Americans dread this - not because they dislike Puerto Rico, but because it would mean fitting one more star on the flag, and ruining its symmetry.  Well, rest easy, America.  Its symmetry is not in jeopardy.  There is already a plan for a 51 star flag that is quite symmetrical.  But this begs the question: what are the techniques for fitting n points (stars) into a rectangle?

Let's start by analyzing the current 50 star flag.  It may surprise you to learn that the arrangement of stars on the 50 star flag has nothing to do with the fact that 50 is a multiple of 10.  The fact that 5 x 10 = 50 does not matter.  The more relevant fact is that (9 x 11 + 1) / 2 = 50, as you will understand in a few minutes.  The 50 star flag is what I call a 'checkerboard' flag.  Checkerboard flags are when you cover the blue region of the flag in a checkerboard pattern, and you put stars only on the white squares.  This is why the 50 star flag seems to be made up of diagonal lines; the diagonal lines are like the lines that a bishop moves along on the chess/checkerboard.


If our checkerboard was, say, 4 rows high and 6 columns wide, it would have 4 x 6 = 24 squares on it.  Since every other square is white, we can count all the white squares by dividing this number by 2.  So, a 4 x 6 checkerboard gives us 24 / 2 = 12 white squares.  This gives us the formula:

Number of stars = rows x columns / 2

Also note that we can swap the colors and have a flag that is a mirror image of the original.

It gets more complicated, though, if the number of squares is an odd number.  If it is an odd number, then you cannot just divide by 2 to get the number of stars - you would not get an integer.  What you do instead is divide it by 2 and then take the integers above and below your answer.  For example, if the number of squares is 99, you would divide by 2 to get 49.5.  Then you would take the integers immediately above and below this answer: 49 and 50.  This means that you can get a 49 star flag or a 50 star flag, depending on which squares you pick to be white.  If you pick the corners to be white, you get a 50 star flag, and if you pick the corners to be black, you get a 49 star flag.

That 9 x 11 pattern with the corners white is the standard pattern for the current United States flag.

This gives us two new equations:

Number of stars = ( rows x columns + 1 ) / 2   (corners white) 
Number of stars = ( rows x columns - 1 ) / 2   (corners black)

There is one more kind of flag we have not talked about.  This is a simple grid flag.  It is like the checkerboard flag except that you put stars in all of the squares, not just the white ones.  The formula for this kind of flag is simple and hardly worth elaborating on:

Number of stars = ( rows x columns )


Putting it All Together:

The goal, now, is to find a suitable pattern for a given number of stars.  So, given 51 stars, what patterns will work?  The mathematics make this easy.  Just solve all of the above equations for rows x columns, like this:

rows x columns = (Number of stars) x 2       even checkerboard flags

rows x columns = (Number of stars) x 2 - 1   odd checkerboard flags, white corners

rows x columns = (Number of stars) x 2 + 1   odd checkerboards flags, black corners

rows x columns = (Number of stars)           simple grid flags

We can use these formulas to find patterns for a 51 star flag.  By plugging 51 into the formulas above, we see that rows x columns can equal 102, 101, 103 or 51, respectively.

Now we need to factor these numbers to see if any are suitable.  101 and 103 are prime numbers, so they will not work.  51 is 17 x 3.  But a 17 x 3 grid flag would be ugly, so 51 will not work.  102 is 17 x 6.  A 17 x 6 checkerboard flag would be just fine!  So there is our answer: a 51 star flag should be a 17 x 6 checkerboard flag:

The 51 star flag, a 17 x 6 checkerboard flag.  You may notice that the checkerboard is squeezed.  It has to fit 17 columns, but only 6 rows.  This pushes the stars together horizontally.  Despite this, the flag still looks good.  Checkerboard flags can handle a lot of squeezing before they start to look funny.

This technique can be used to find suitable flags for all the numbers from 50 to 100 except 62, 79 and 89.  Many flags have several suitable arrangements.  Here are arrangements for flags 51 to 70:

Now you must be wondering what you can do with a 62, 79 or 89 star flag.  Actually, there are plenty of options.  But that is for another post.

You will notice that there are only five simple grid flags in the above display: 54, 60, 63, 66 and 70.  Good grid flags are quite a bit more scarce than good checkerboard flags.  And, frankly, I do not think that grid flags look very good.  All of the grid flags shown here could be replaced with checkerboard flags of the same number of stars.  I chose to use the grid flags in this display for the sake of diversity, but if it were up to me, they would all be checkerboard style.  The only grid flag that I like is the 48 star 6 x 8 grid flag, and that is only because it was used in World War II, and raised in the famous photo at Iwo Jima.

There are a couple more interesting styles of flag, but they will be left for a later post.  If just one reader sleeps more easily knowing that we do not have a 51-star flag crisis looming, my work here is done.